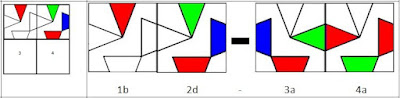
Backtracking ist ein Algorithmus, der zur Lösung vieler
Geduldspiele angewendet werden kann. Dazu gehören viele Legespiele und
Packprobleme, solange sie auf einem regelmäßigen Gitter im zwei- oder
dreidimensionalen Raum stattfinden. Als Beispiel sollen uns
ein kleines Edge-Matching Puzzle sowie eine kleine Pentomino-Aufgabe dienen. Aber Backtracking ist
beispielweise auch auf Sudoku anwendbar oder für das Acht-Damen-Problem auf
dem Schachbrett.
Die zu lösenden Probleme müssen folgende Eigenschaften haben:
-
Es gibt ein Feld (meist ein Teil aus einem regelmäßigen Gitter, z.B. ein
Rechteck mit ganzzahligen Seitenlängen), welches mit Objekten belegt werden
soll.
-
Dazu gibt es eine Menge von Objekten. Jedes Objekt füllt entsprechend seiner
Form eines oder mehrere Elementarzellen des Gitters. Manchmal können die
Objekte in verschiedenen Orientierungen verwendet werden, diese entstehen
durch Drehen und/oder Wenden der Objekte (Wenden nur im zweidimensionalen
Fall).
-
Ein Objekt kann auf dem Feld an einer bestimmten Stelle platziert werden,
wenn die entsprechenden Elementarzellen auf dem Feld frei sind (z.B. im
Falle von Pentominos) und möglicherweise benachbarte Objekte zusammenpassen
(wie bei Edge-Matching Puzzles).
Dazu kommen noch zwei technische Anforderungen für die Kodierung des Problems:
-
Die Elementarzellen des Feldes werden von eins beginnend durchnummeriert.
Die Reihenfolge der Nummerierung ist zunächst egal, aber praktisch ist eine
zeilenweise Nummerierung von oben nach unten.
-
Auch die Objekte werden nummeriert. Falls mehrere Orientierungen möglich
sind, wird ein Buchstabe angefügt, der die Orientierung beschreibt (z.B.
beschreibt 2a das zweite Objekt in der ersten Orientierung).
Dies ermöglicht es uns, die zu einem bestimmten Moment möglichen Züge in eine
Reihenfolge zu bringen. Haben wir bereits einige Objekte auf dem Feld
platziert, so verfügen wir über eine Menge noch nicht überdeckter Felder und
eine Menge übriger Steine.
Der Einfachheit halber wollen wir noch zwei weitere Annahmen machen. Diese
vereinfachen den Algorithmus etwas, aber eine etwas kompliziertere Variante
des Backtracking kann darauf auch verzichten.
-
Die Steine dürfen nicht rotiert oder gewendet werden, sind also in der
vorliegenden Orientierung zu verwenden.
-
Außerdem soll das Feld vollständig gefüllt werden, es bleiben also keine
freien Felder. Damit lassen sich sogenannte Sackgassen (s.u.) leichter
erkennen.
Wir bringen die nun möglichen Züge in die folgende Reihenfolge:
-
Betrachtet werden nur Züge, die das Feld mit der kleinsten unüberdeckten
Nummer bedecken.
-
Diese Züge ordnen wir nach der Nummer des jeweils verwendeten Steins (im
allgemeinen Fall ggf. zusätzlich mit Orientierung), der das Feld überdecken
wird.
Der nun folgende Algorithmus platziert die Objekte in allen möglichen
Varianten auf dem Feld. Dadurch werden alle möglichen Lösungen gefunden.
Darüber hinaus erkennt der Algorithmus Sackgassen, die es nicht weiter zu
verfolgen lohnt. Dabei versteht man unter einer Sackgasse Folgendes: Wenn wir
das komplette Feld bedecken sollen und beispielsweise bemerken, dass wir kein
Objekt mehr zur Verfügung haben, um eine leeres Elementarzelle oben rechts zu
bedecken, dann sind wir in einer Sackgasse. Da nützt es gar nichts, mit dieser
Teillösung weiterzumachen und weitere Objekte an andere Stellen des Feldes zu
legen, wir werden wegen der leer bleibenden Elementarzelle oben rechts niemals
das ganze Feld füllen können.
Zu jedem Zeitpunkt gibt es eine Menge der noch einzufügenden Steine. Diese
Steine sind immer entsprechend ihrer Nummer sortiert. Einer der Steine ist
gerade ausgewählt und soll eingefügt werden. Wenn das nicht möglich ist (weil
er nicht da nächste freie Feld bedecken kann), muss eine neue Auswahl
getroffen werden, dies ist der nächste Stein aus der Menge der noch
einzufügenden Steine.
Wir wollen uns zuerst eine etwas umständlichere Variante des Algorithmus
ansehen. Das eigentliche Backtracking werden wir erst später einbauen.
Zunächst schauen wir uns alle möglichen Reihenfolgen in ihrer natürlichen
Reihenfolge an, in welcher wir die Steine verwenden können. Diese Reihenfolge
sagt uns dann, wohin jeder Stein gelegt wird, weil immer das nächste freie
Feld überdeckt werden soll.
Nehmen wir an, wir haben neun Steine; dann gibt es eine lange Reihe von
9!=362.880 verschiedene Reihenfolgen, die wir nacheinander durchprobieren
könnten:
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 9 8
1 2 3 4 5 6 8 7 9
...
9 8 7 6 5 4 3 2 1
Die allermeisten von diesen Reihenfolgen führen nicht zu einer Lösung, und in
der Regel merken wir das relativ schnell. Betrachten wir ein Beispiel: Wir
beginnen mit der Reihenfolge 1 2 3 4 5 6 7 8 9 und nehmen an, dass wir zwar
die ersten zwei Steine korrekt platzieren können, aber der Stein Nummer 3
nicht passt. Dann brauchen wir uns die Steine 4 bis 9 gar nicht mehr
vorzunehmen:
Wenn Stein 3 nicht passt, dann sind die folgenden
Reihenfolgen sämtlich keine Lösung:
1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7
9 8
...
1 2 3 9 8 7 6 5 4
Dies sind 6!=720 Zeilen, die in der oben erwähnten langen Reihe unmittelbar
hintereinander stehen. Diese können alle übersprungen werden. Durch diesen
Trick sparen wir sehr viele Versuche und der Algorithmus kommt in der langen
Reihe schnell voran: Wenn der Anfang 1 2 3... nicht zu einer Lösung führt,
probieren wir den nächsten Anfang 1 2 4... Jetzt nehmen wir einmal an, auch
das passt nicht und die nachfolgenden Versuche mit 1 2 5..., 1 2 6..., 1 2
7...,1 2 8... und 1 2 9... passen auch nicht. Dann konnten wir nach dem ersten
Stein zwar den zweiten einfügen, aber es ging nicht weiter. Also versuchen wir
in unserer langen Reihe den nächsten möglichen Anfang, das ist 1 3.... Die
erste Zeile in der langen Reihe mit diesem Anfang ist 1 3 2 4 5 6 7 8 9, dies
ist die Zeile mit der Nummer 5040. Wir haben bisher sieben (vergebliche)
Versuche gemacht und schon mehr als fünftausend Zeilen aus der langen Liste
abgearbeitet. Je schneller sich eine Reihenfolge als unbrauchbar herausstellt,
desto größer ist der übersprungene Block in der langen Liste. Falls also
beispielsweise 1 3... nicht passt, geht es gleich weiter mit 1 4... und mit
einem Versuch wurden weitere 5040 Zeilen übersprungen. Und wenn es eine
Reihenfolge gibt, die zu einer Lösung führt, wird diese natürlich auch
gefunden.
Der Backtracking-Algorithmus legt nun nicht wie im obigen Beispiel zuerst die
sehr lange Liste an, sondern erzeugt nacheinander nur die wirklich zu
betrachtenden Anfänge, in unserem Beispiel von oben wäre das
1 2 3
1 2 4
1 2 5
1 2 6
1 2 7
1 2 8
1 2 9
1
3
1 4
...
Wir wollen uns das genaue Verhalten von
Backtracking noch an einem einfachen Edge Matching Puzzle
ansehen.
Mehr Infos: