Am folgenden einfachen Geduldspiel soll Backtracking erklärt werden: Gegeben sind vier Karten für ein 2x2-Anlegepuzzle. Da hier eine Rotation der Karten erlaubt ist, muss dies auch beim Backtracking berücksichtigt werden.
Diese Karten sollen so in ein 2x2-Quadrat gelegt werden, dass sich an den Trennlinien jeweils einfarbige Dreiecke ergeben. Diese Quadrate mit den Nummern 1 bis 4 können noch mehrfach um 90 Grad (im Uhrzeigersinn) gedreht werden, diese Orientierungen werden mit a (wie abgebildet), b, c und d bezeichnet. Die Karte 2c ist also die Karte Nr. 2 um 180 Grad gedreht.
Die Felder des Geduldspiels sind ebenfalls mit 1 bis 4 durchnummeriert und sollen in dieser Reihenfolge nacheinander belegt werden:
Der Backtracking-Algorithmus startet mit dem leeren Rahmen und einer Reihe zunächst aller Karten. in alphabetischer Reihenfolge (Bild 1: - 1a 2a 3a 4a). Das Minuszeichen in der Liste steht vor der aktuellen Bearbeitungsposition, bisher ist nichts eingefügt.
Die vorderste Karte der Reihe wird (in der aktuellen Orientierung) in das erste (freie) Feld im 2x2-Rahmen erfolgreich eingefügt. (Bild 2: 1a - 2a 3a 4a)
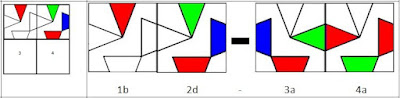
Danach ist die Bearbeitungsposition um eins nach rechts verschoben. Wieder soll die nun vorderste Karte nach der Bearbeitungsposition (in der aktuellen Orientierung) in das nächste freie Feld (also Feld Nummer 2) eingefügt werden. Das funktioniert nicht wegen des falschen Bildes an der linken Kante. Also wird die nächste Orientierung der aktuellen (also der zweiten) Karte versucht. Diese und die dritte funktionieren auch nicht, aber die vierte Orientierung funktioniert. Bild 3: 1a 2d - 3a 4a
Nun soll die nächste (dritte) Karte in das nächste (dritte) Feld eingefügt werden. Das klappt weder in der angegebenen ersten Orientierung noch in einer anderen. Außerdem ist noch die vierte Karte in der Liste, diese könnten wir auch an Position drei legen. Aber auch das passt in keiner Orientierung. Damit sind wir in einer Sackgasse und jetzt beginnt das eigentliche Backtracking:
Da wir an der dritten Position keine Karte mehr einfügen können, ist schon vorher eine unlösbare Situation eingetreten. War dies bei der zweiten Karte der Fall? Nein, da haben wir alle Orientierungen durchprobiert. Also müssen wir gleich bei der ersten Karte etwas ändern. Diese haben wir an dieser Stelle noch nicht in allen Orientierungen benutzt und wir drehen sie deshalb um 90 Grad (Bild 4: 1b - 2a 3a 4a).
Jetzt muss wieder Position 2 gefüllt werden. Die zweite Karte in der aktuellen Orientierung (2a) passt nicht, ebensowenig 2b und 2c. Allerdings passt wieder 2d (Bild 5: 1b 2d - 3a 4a).
Jetzt muss Position 3 gefüllt werden. Die nächste Karte passt sofort unter die erste Karte (Bild 6: 1b 2d 3a - 4a).
Für die verbleibende Position 4 passt zwar nicht die Karte 4a, aber nach einer Rotation der Karte passt 4b.
Damit haben wir eine Lösung gefunden: (Bild 7: 1b 2d 3a – 4b).
In der Notation des allgemeinen Backtracking haben wir damit von den vielen Möglichkeiten in alphabetischer Reihenfolge nur die folgenden Möglichkeiten betrachtet:










Keine Kommentare:
Kommentar veröffentlichen