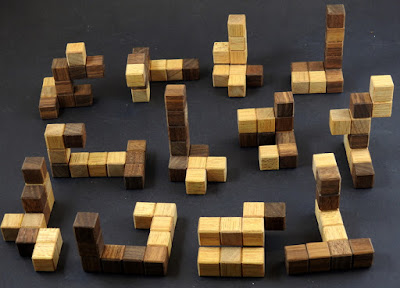Zwölf Polykuben, die jeweils aus zehn Elementarwürfeln bestehen (sollen sie Dekomino heißen?), müssen in einen 5x5x5-Würfel gepackt werden. Die fünf verbleibenden Elementarwürfel sollen ein Loch von der Mitte einer Seite zur gegenüberliegenden Seitenmitte bilden, dies ist das namensgebende Wurmloch. Zusätzlich haben die Elementarwürfel zwei verschiedene Farben, die Kantenwürfel des 5x5x5-Würfels sind dunkler als die Seitenwürfel; die Innenwürfel sind scheinbar zufällig gefärbt.
Schwierigkeit: Die Polykuben sind groß im Vergleich zu anderen Geduldspielen. Das freibleibende Wurmloch sorgt zusätzlich für Schwierigkeiten, zusammenpassende Steine zu finden. Das schränkt die Anzahl der möglichen Lösungen ein, macht es aber nicht einfacher, sie zu finden. Es wurde berichtet, dass dieses Geduldspiel noch von keinem Menschen ohne Zuhilfenahme eines Computers gelöst wurde [1].
PolySolver-Info: Der PolySolver kann natürlich helfen. Wir haben mindestens drei Möglichkeiten.
Variante 1: Wir können die fünf Elementarwürfel frei lassen. Dann müssen wir bei den gefundenen Lösungen schauen, ob die fünf Elementarwürfel das verlangte Wurmloch bilden.
Variante 2: Alternativ können wir einen zusätzlichen stabförmigen Stein aus fünf Elementarwürfeln hinzunehmen und bei Lösungen schauen, wo sich das Wurmloch befindet.
Variante 3: Schließlich könnte auch der 5x5x5-Würfel um das Wurmloch verkleinert werden.
Bevor wir uns für eine der Varianten entscheiden, können wir vorher darüber nachdenken, welche der drei Methoden die Lösungen am schnellsten findet. In der oben angegebenen Reihenfolge wird der PolySolver jeweils merklich schneller, weil er weniger Optionen durchprobieren muss: Bei Variante 1 wird zusätzlich nach Lösungen mit einzelnen leeren Elementarwürfeln gesucht. Dadurch entstehen viel mehr Teillösungen, die erst später wieder verworfen werden. Bei Variante 2 wird versucht, das Wurmloch auch an anderer Stelle zuzulassen, aber immerhin als zusammenhängendes, stabförmiges Loch. Das sind weniger Optionen als bei Variante 1, aber immer noch mehr als nötig: Variante 3 lässt das Wurmloch nur an der gewünschten Stelle zu.
In jedem der drei Fälle gibt es bis auf Symmetrie nur eine einzige Lösung, die Methoden 1 und 2 finden keine zusätzlichen Lösungen, suchen aber länger. Dies entspricht jeweils 24 PolySolver-Lösungen.
PolySolver-Dateien: Hier sind die PolySolver-Dateien für die drei oben angegebenen Modellierungsvarianten zusammen mit der Laufzeit auf einem normalen PC.
- Variante 1: Der PolySolver benötigt 41 Minuten.
- Variante 2: Der PolySolver benötigt 43 Sekunden.
- Variante 3: Der PolySolver benötigt 1.3 Sekunden.
Wie erfindet man ein solches Geduldspiel? Genau wissen wir es nicht, aber wir bekommen einen Hinweis, wenn wir uns die Polykuben genauer ansehen: Jeder dieser Steine ist zusammengesetzt aus zwei ebenen Pentominos. Wir könnten zunächst ein einfacheres Geduldspiel mit den entsprechenden Pentominos lösen und danach jeweils zwei benachbarte Pentominos zusammenkleben. Allerdings können wir uns so nicht sicher sein, wie schwierig es ist, eine Lösung unserer Variante von Watson's Wormhole zu finden. Auch kann es mehrere Lösungen geben.
Die Steine im Bild setzen sich dabei aus den folgenden Pentominos zusammen:
- obere Reihe: FT, FL, NX und PI,
- mittlere Reihe: UT, IX, US und WY,
- untere Reihe: WP, LV, NV und SY.
Erscheinungsjahr: 2000
Shopping: Nur selten gebraucht erhältlich.