Kategorie: Schiebepuzzles mit Polyominos (systematisch)
Es war vermutlich der japanische Puzzledesigner Minoru Abe, der auf die Idee kam, dass man die üblichen Schiebespiele nicht nur in einem rechteckigen Rahmen spielen kann, sondern dass auch ein gezackter Rand möglich ist. Minoru Abe hat das Rechteck am oberen Rand um einen oder zwei Steine in der Mitte erweitert, wir wollen beliebige symmetrische Muster am oberen Rand erlauben und die hervorstehenden Felder als Zinnen bezeichnen. Das abgebildete Feld hat also eine breite Zinne. Es besteht aus nur 13 Feldern, allzu komplizierte Schiebespiele sind also nicht zu erwarten.
Das nächstgrößere rechteckige Feld hat die Größe 3x5. Die interessantesten Schiebespiele auf dem 3x5-Rechteck wurden bereits vorgestellt, hier auf dem kleineren Spielfeld sind noch einfachere Spiele zu erwarten.
Wie immer konzentrieren wir uns auf optisch oder konzeptionell interessante Spiele. Die Bilder zeigen jeweils die Start- und Zielkonfiguration eines Schiebespiels, darüber steht die Anzahl der benötigten Züge (jeweils ein Stein wird um eine Position bewegt). Die Beschreibung dazu erklärt den Typ des Spiels, ist aber keine vollständige Beschreibung.
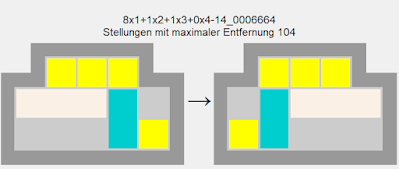
Aufgabe 1 - Schwierigste Aufgabe; Spiegeln: Dies ist die Aufgabe mit den meisten Zügen. Das Problem besteht darin, dass der stehende Dominostein die Bewegung der waagerechten Dominos stark behindert.
Aufgabe 2 - Spiegeln: Mit vier Leerfeldern ist diesmal viel Platz, aber die zwei großen Steine behindern sich gegenseitig.
Aufgabe 3 - Spiegeln / Wandern: Optisch sind Start und Ziel gespiegelt. Aber um das zu erreichen, muss nur ein gelbes Quadrat von links nach rechts wandern.
Aufgabe 4 - Spiegeln / Wandern: Optisch sind Start und Ziel gespiegelt. Aber um das zu erreichen, muss nur der stehende Dominostein von rechts nach links wandern.
Aufgabe: 5 - Wandern: Hier soll der liegende Dominostein von unten nach oben wandern, und die gelben Quadrate nach rechts..
Aufgabe 6 - Spiegeln: Sieht auf den ersten Blickeinfach aus, aber wie sollen die gelben Quadrate jeweils die Seiten wechseln?
Aufgabe 7 - Spiegeln: Eigentlich müssen nur die zwei Steine in der unteren Reihe ihre Plätz tauschen.
Aufgabe 8 - Spiegeln: Wie in der vorigen Aufgabe, nur liegen die großen Steine eine Etage höher..
Aufgabe 9 - Spiegeln: Drei kleine Quadrate von rechts nach links.
Aufgabe 10 - Spiegeln: Diesmal sind sogar fünf Felder frei. Dies ist die schwierigste Aufgabe mit so viel Platz.
Aufgabe 11 - Aufräumen: Zwei gelbe Quadrate müssen von links nach rechts. Aber Domino und Winkel blockieren in der ganzen Höhe.
Aufgabe 12 - Aufräumen: Diesmal ist auch ein L-Stein aus vier Elementarquadraten involviert. Dies ist die schwierigste Aufgabe mit einem L.














Keine Kommentare:
Kommentar veröffentlichen