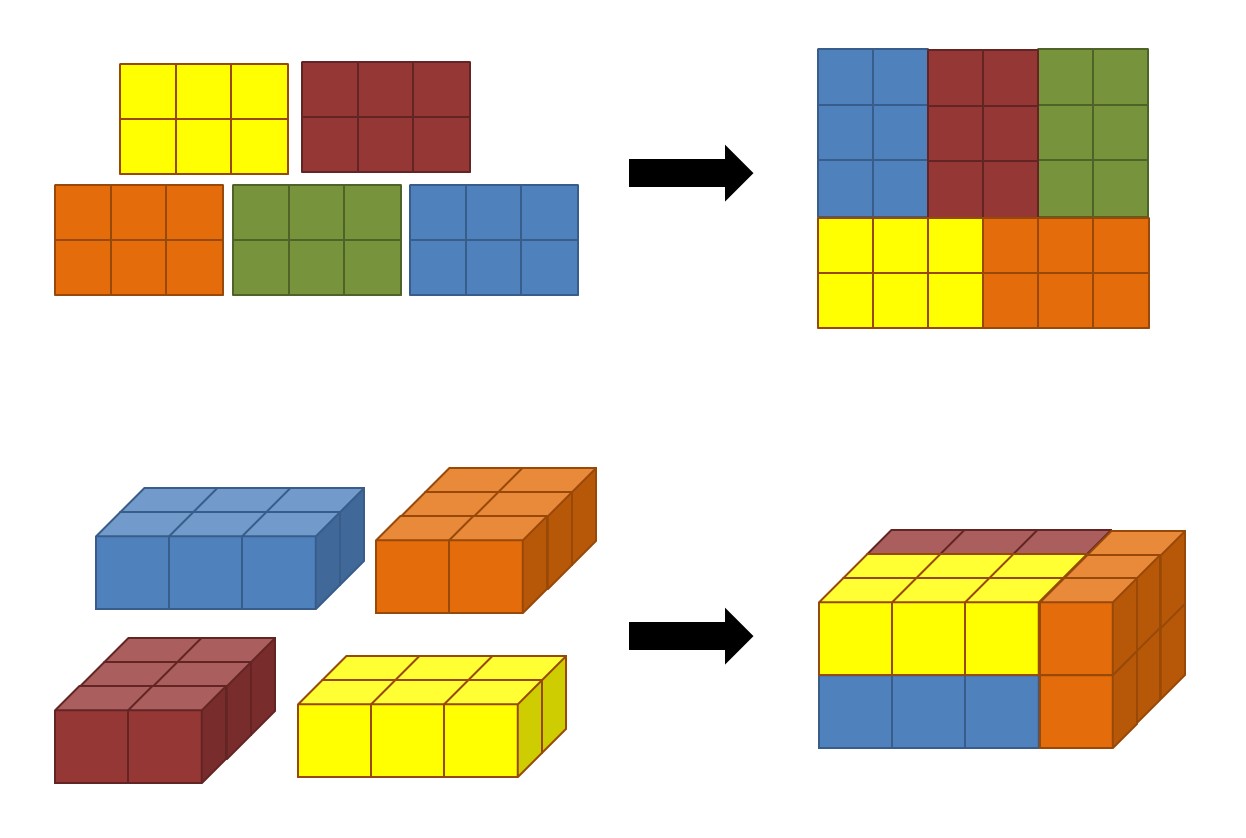
Kategorie: Gleiche Klötzer in rechtwinklige Boxen packen
Eigentlich könnte man hoffen, dass 42 Klötzer der Größe 1x2x4 in einen 7x7x7-Würfel passen und dann noch sieben Elementarwürfel frei bleiben. Das klappt aber leider nicht, wie schon im Jahr 1976 gezeigt wurde [1]. Aber mit 41 statt 42 klappt es:
Aufgabe: Packen Sie 41 Klötzer der Größe 1x2x4 und 15 Elementarwürfel in einen 7x7x7-Würfel! Wenn Sie es noch etwas schwieriger haben wollen: Es klappt auch mit 4 Stück 1x1x3 plus drei Elementarwürfeln statt der 15 Einzelwürfel.
Auch wenn wir wissen, dass es sich um eine lösbare Aufgabe handelt, kommt man durch Herumprobieren nicht zum Ziel. Gibt es vielleicht einfachere Teilaufgaben? Im Schnitt dürfen in einer Schicht von 7x7 Würfeln reichlich zwei Elementarwürfel frei bleiben. Bei geradzahliger Höhe geht es aber besser: Wir können es relativ einfach schaffen, dass nur ein Elementarwürfel pro Schicht frei bleibt, und zwar genau der mittlere Elementarwürfel. Hier das Bild für 7x7x2:
Verringern wir also die Höhe um zwei, müssen wir einen 5x7x7-Quader mit 29 Steinen der Größe 1x2x4 füllen. Vielleicht scheint dies für den Menschen auf den ersten Blick nicht einfacher zu sein, aber der Computer zeigt mit dem PolySolver einen dramatischen Unterschied.
PolySolver-Info: Für die 7x7x7-Aufgabe findet der PolySolver innerhalb 10 Minuten rund 60.000 Lösungen (und würde noch mehr finden), die erste Lösung findet er nach sechseinhalb Minuten. Bei der "etwas kleineren" 5x7x7-Aufgabe findet der PolySolver blitzartig die erste Lösung und sofort weitere.
Um es für uns Menschen noch einfacher zu machen: Klappt derselbe Trick noch einmal, d.h. können wir einen 7x7x3-Quader mit 17 Steinen der Größe 1x2x24 füllen? Leider nein! Damit sind 2x7x7 und 5x7x7 die einzigen Schichthöhen, die wir unter den gegebenen Nebenbedingungen mit 1x2x4-Steinen füllen können.
Anders als beim Theorem von De Bruijn, dass uns nur sagt, wann eine Box sich vollständig mit Steinen gleicher Größe füllen lässt (oder auch nicht), ist die Situation bei den speziellen Steinen der Größe 1x2x4 noch besser: F.W. Barnes beschreibt in [2] genau, wie viele solche Steine in eine beliebige Box mit ganzzahliger Seitenlänge passen und wie viele Elementarwürfel übrigbleiben müssen. Wir werden darauf noch zurückkommen.
Mehr Infos:
[1] M. Mather: Solution to Problem E2524, Amer. Math. Monthly 83 (1976) S. 741-742.
[2] F.W. Barnes: How many 1×2×4 bricks can you get into an odd box?. Discrete Mathematics Vol. 133, Pages 55-78, Elsevier 1994