Übersicht: Gleiche Klötzer in rechtwinklige Boxen packen

Viele gleiche Klötzer sollen in eine rechtwinklige Box passender Größe gepackt werden. Klötzer packen können wir in zwei oder drei Dimensionen: Die Klötzer sind entweder Rechtecke (2D) oder Quader (3D), die Boxen ebenfalls Rechtecke oder Quader. Es sollen jeweils eine bestimmte Anzahl gleicher Klötzer eingepackt werden, die Seitenlängen der Klötzer sind ganzzahlig. Bei den meisten Aufgaben sollen die Boxen vollständig gefüllt werden. Manchmal bleiben auch einige Elementarwürfel frei oder sollen mit zusätzlichen kleinen Steinen gefüllt werden. Es gibt auch unlösbare Aufgaben, bei denen sich die Klötzchen einfach nicht einpacken lassen wollen und man diese Unmöglichkeit auch beweisen kann.

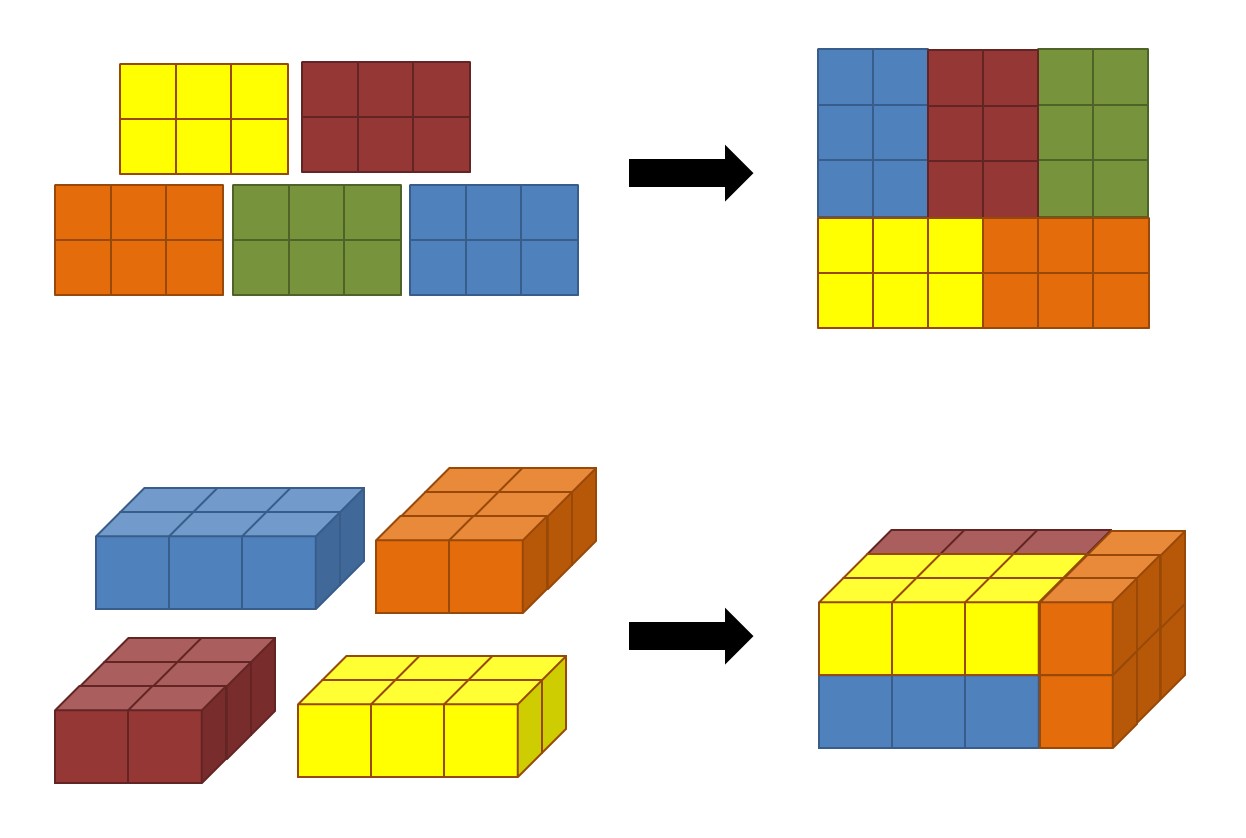
	Rechtecke packen Viele gleiche Rechtecke in eine Box passender Größe zu packen, sieht einfach aus, ist manchmal aber sehr vertrackt oder gar unmöglich. Ein wenig Theorie hilft manchmal.

• Einfach oder gar nicht für Rechtecke der Form 1xn: Das Theorem von D.A. Klarner.

Aufgaben Manche Aufgaben sind relativ einfach, andere so schwierig, dass der Computer helfen muss.

• 21 I-Trominos auf Schachbrett
• Erscheint im Dezember: Schwierig für Mensch und Computer: 147 Rechtecke der Größe 95x137 in ein Rechteck der Größe 1230x1600 packen

Unlösbare Aufgaben Findet selbst der Computer keine Lösung, kann man versuchen, die Unlösbarkeit zu beweisen. Hilfreich sind oft Färbungen mit einem Schachbrett- oder einem anderen Muster.

• Unlösbare Schachbrettaufgabe: 31 Dominos auf einem Schachbrett, bei dem zwei gegenüberliegende Ecken entfernt wurden.
• 21 I-Trominos auf Schachbrett, bei dem eine Ecke entfernt wurde.
• Unlösbar: Ein 10x10-Quadrat füllen mit 1x4-Stäben

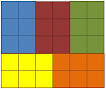
	Quader packen Auf den ersten Blick sieht die dreidimensionale Version des Packproblems nicht viel anders aus als die zweidimensionale. Aber es gibt aus kombinatorischer Sicht mehr Möglichkeiten und andere theoretische Resultate.

• Das Theorem von de Bruijn für harmonische Steine: Einfach oder gar nicht.
• Das Kriterium von N. de Bruijn für beliebige Steine

Lösbare Aufgaben Manche Aufgaben sind relativ einfach, andere so schwierig, dass der Computer helfen muss. Bei umfangreicheren Aufgaben kommt auch der Computer schnell an seine Grenzen

• Conway-Würfel: 6 Stück 1x2x2 in 3x3x3
• Würfelpack
• Eine 6x6x6-Box von Patrick Hamlyn
• Eine 5x6x6-Box füllen mit 44 Stäben der Größe 1x1x4 (und einigen Leerstellen)
• Singmaster Packing: 25 Klötzer der Größe 1x3x4 in einen 5x5x12-Quader
• Packen Sie 41 Klötzer der Größe 1x2x4 und 15 Elementarwürfel in einen 7x7x7-Würfel
• 14 Quader der Größe 1x2x4 in eine 5x5x5-Kiste packen plus 3 Stück 1x1x4

Unlösbare Aufgaben Findet man keine Lösung, kann man versuchen, die Unlösbarkeit zu beweisen. Hilfreich sind wieder Färbungen oder das Theorem von de Bruijn.

• Unmöglich: 15 Quader der Größe 1x2x4 in eine 5x5x5-Kiste packen
• Eine 5x6x6-Box füllen mit 45 Stäben der Größe 1x1x4
• 54 Stäbe 1x1x4 in 6x6x6
• 27 Klötzer 1x2x4 in 6x6x6